Chi Square Definition Math

The chi square distribution has the following properties.

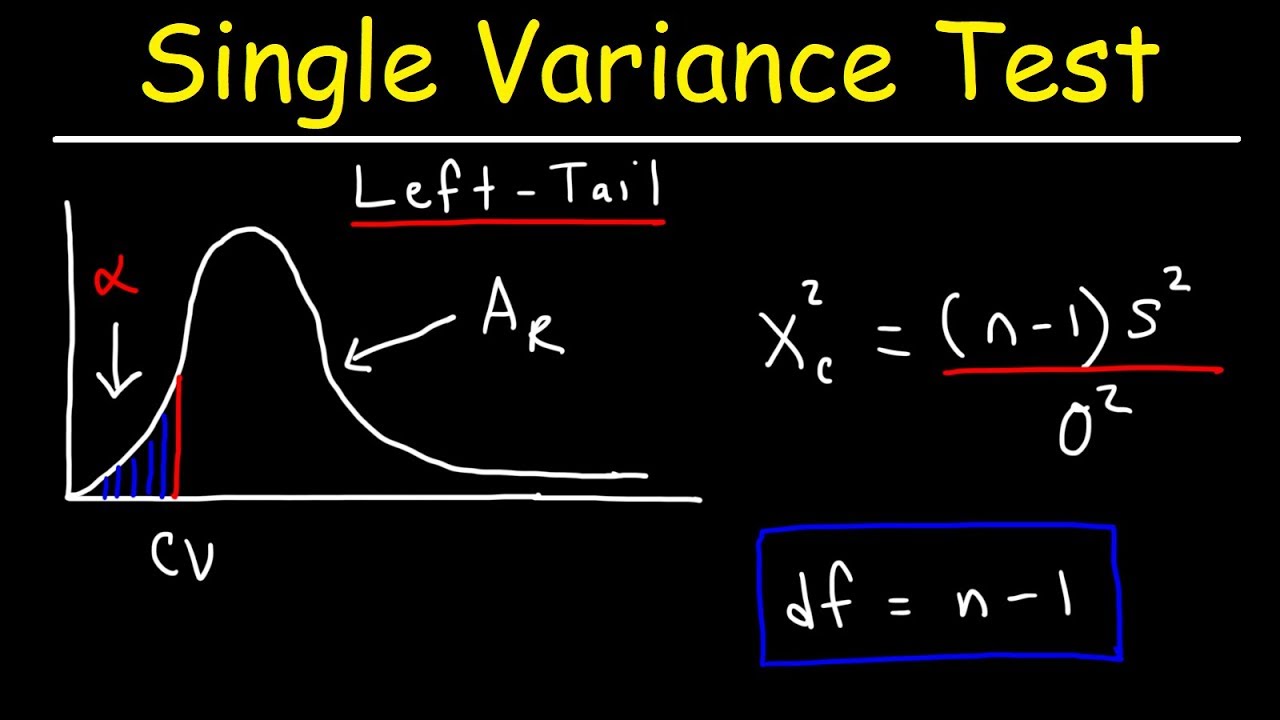
Chi square definition math. The chi square distribution is a building block of many types of statistical hypothesis testing such as chi square tests for goodness of fit and variation anova via the f distribution and the t distribution. The chi square distribution is a special case of the gamma distribution and is one of the most widely used probability distributions in inferential statistics notably in hypothesis testing and in construction of confidence intervals. In probability theory and statistics the chi square distribution with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables. A chi square goodness of fit test is used to determine whether or not a categorical variable follows a hypothesized distribution.

The formula to perform a chi square goodness of fit test. χ2 depends on the size of the difference. A chi square χ2 statistic is a measure of the difference between the observed and expected frequencies of the outcomes of a set of events or variables. In probability theory and statistics the chi square distribution also chi squared or distribution is one of the most widely used theoretical probability distributions in inferential statistics i e.

In statistical significance tests. In the following chi square calculation formula x represents chi while o and e represent the. Chi square is a calculation used to determine how closely the observed data fit the expected data. The motivation for performing a chi square goodness of fit test.

A statistic that is a sum of terms each of which is a quotient obtained by dividing the square of the difference between the observed and theoretical values of a quantity by the theoretical value first known use of chi square 1900 in the meaning defined above. This tutorial explains the following.