Define Converging Math

Otherwise it is called divergent.

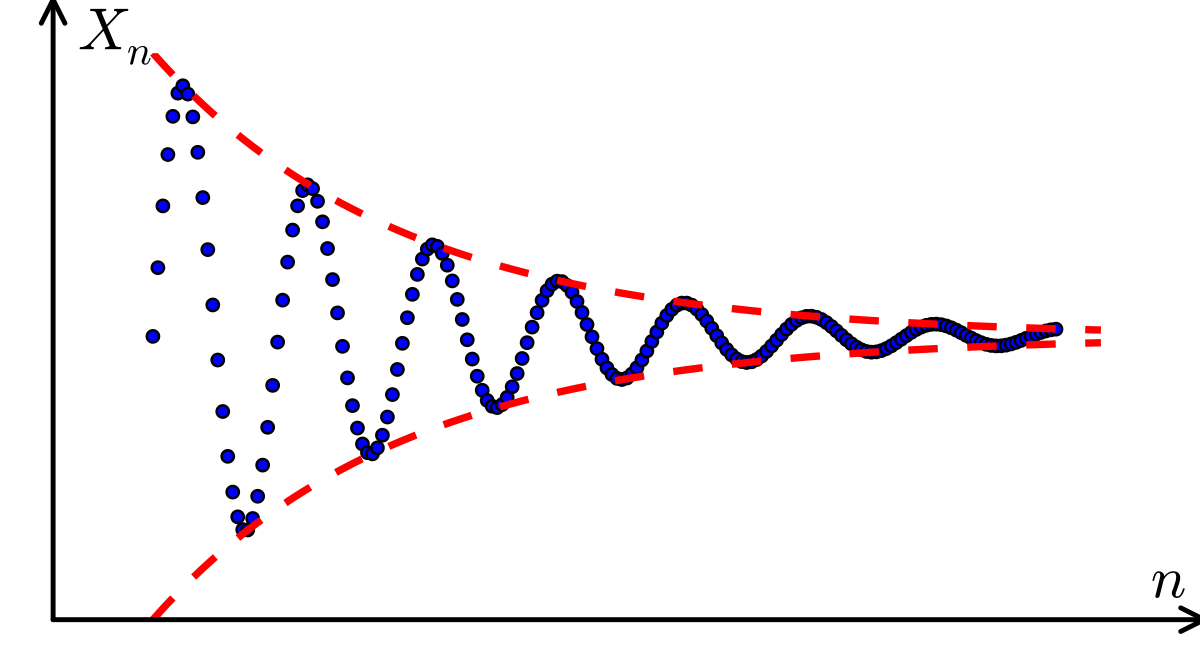
Define converging math. Of an infinite series to have a finite sum. A town at the convergence of two rivers. To have a sequence of partial sums that converges. This leads us to the first of many tests for the convergence divergence of a series that we ll be seeing in this chapter.

Of a sequence to have values eventually arbitrarily close to some number. When a sequence does have a limit that is a number and exists we call it a convergent sequence. That means that the partial sums become closer and closer to a given number when the number of their terms increases. For example the function y 1 x converges to zero as x increases.

Physiology the coordinated turning of. The act condition quality or fact of converging. Math explained in easy language plus puzzles games quizzes videos and worksheets. If the series terms do not go to zero in the limit then there is no way the series can converge since this would violate the theorem.

More precisely a series converges if there exists a number ℓ displaystyle ell such that for every arbitrarily small positive number ε displaystyle varepsilon there is a sufficiently large integer n displaystyle n. The point of converging. Every infinite sequence is either convergent or divergent. A convergent sequence has a limit that is it approaches a real number.

A series which have finite sum is called convergent series otherwise is called divergent series. To have a finite limit. Convergence in mathematics property exhibited by certain infinite series and functions of approaching a limit more and more closely as an argument variable of the function increases or decreases or as the number of terms of the series increases. To determine if a given sequence is convergent we use the following two steps.

In order for a series to converge the series terms must go to zero in the limit. For k 12 kids teachers and parents. Verb used without object con verged con verg ing. Mathematics the property or manner of approaching a limit such as a point line function or value.

Of an improper integral to have a finite value. Here s an example of a convergent sequence. A series is convergent if the sequence of its partial sums s 1 s 2 s 3 displaystyle s 1 s 2 s 3 dots tends to a limit.