Np Complete Vs Np Hard Math

Euler diagram for p np np complete and np hard set of problems.

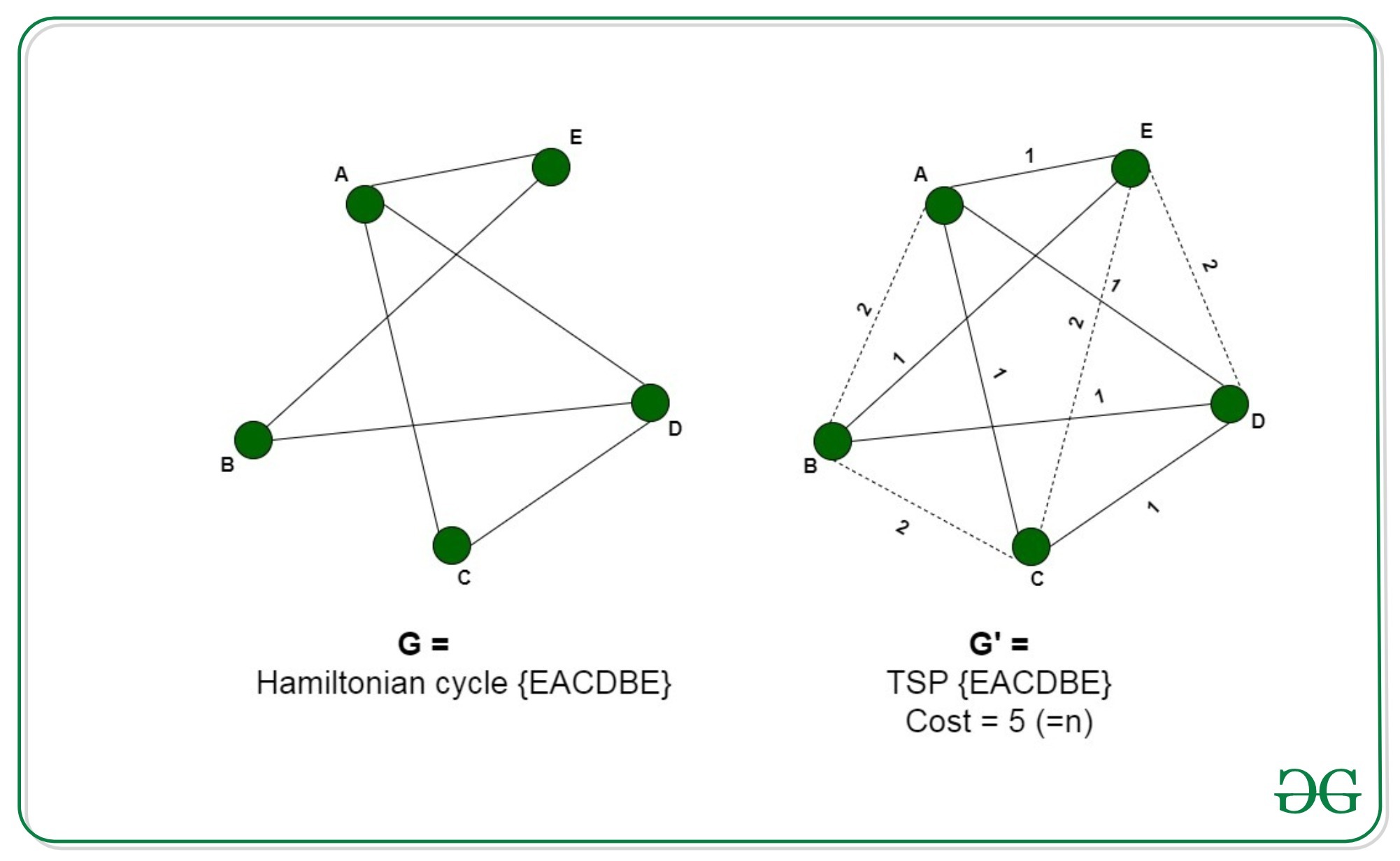
Np complete vs np hard math. Np complete problem any of a class of computational problems for which no efficient solution algorithm has been found. So called easy or tractable problems can be solved by computer algorithms that run in polynomial time. A diagram showing the relevant complexity classes in the p vs np problem. It is like saying there are things that people can do p there are things that superpeople can do sp and there are things only superpeople can do sp complete.

I e for a. Np complete problems can be solved by deterministic algorithm in polynomial time. Np problems might be solvable in polynomial time and are checkable in. So the easy problems are in p and np but the really hard ones are only in np and they are called np complete.

To solve this problem it must be a np problem. P problems are solvable in polynomial time. The left side is valid under the assumption that p np while the right side is valid under the assumption that p np except that the empty language and its complement are never np complete in computational complexity theory np hardness non deterministic polynomial time hardness is the defining property of a class of problems that are informally at least as hard as the hardest problems in np.