Sample Variance Vs Population Variance Math

But it s a particular type of sample variance where we just divide by the number of data points we have.

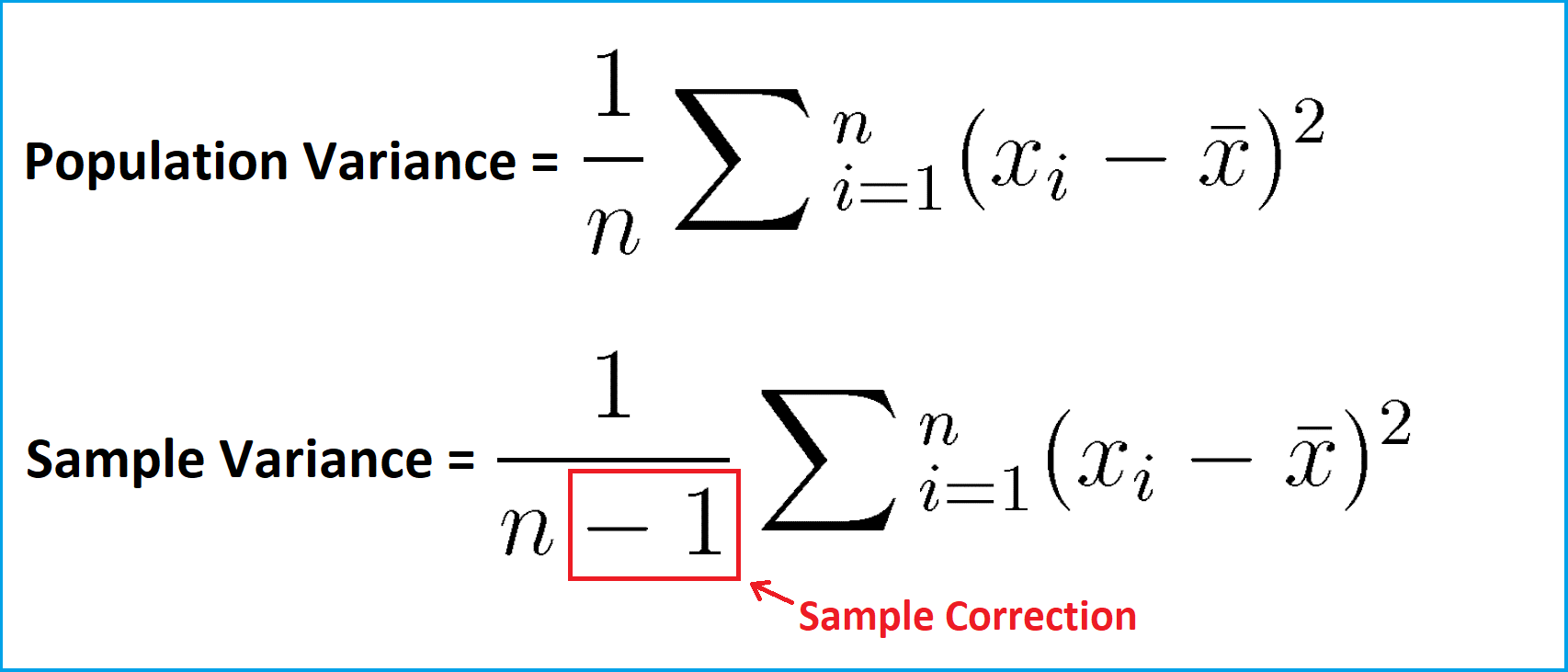
Sample variance vs population variance math. As a result the calculated sample variance and therefore also the standard deviation will be slightly higher than if we would have used the population variance formula. Divide by n when calculating variance like we did a sample. Using the formula with n 1 gives us a sample variance which on average is equal to the unknown population variance. Or maybe i will call that thing the variance.

And so people will write just an n over here. The purpose of this little difference it to get a better and unbiased estimate of the population s variance by dividing by the sample size lowered by one we compensate for the fact. What if we did the computation with n instead of n 1. When i calculate population variance i then divide the sum of squared deviations from the mean by the number of items in the population.

Divide by n 1 when calculating variance. And so what i do so the variance and i will do and this is a population variance that i m talking about just to be clear it s a parameter. Due to this value of denominator in the formula for variance in case of sample data is n 1 and it is n for population data. So also with few samples we can get a reasonable estimate of the actual but unknown parameters of the population distribution.

Sample variance there is only one little difference in the calculation of variance and it is at the very end of it. The population variance i m going to denote with the greek letter sigma lowercase sigma this is capital sigma lowercase sigma squared. In our example 2 i divide by 99 100 less 1. When dealing with the complete population the population variance is a constant a parameter which helps to describe the population.

Population variance refers to the value of variance that is calculated from population data and sample variance is the variance calculated from sample data. And sometimes this will be called the sample variance. The difference in calculation.