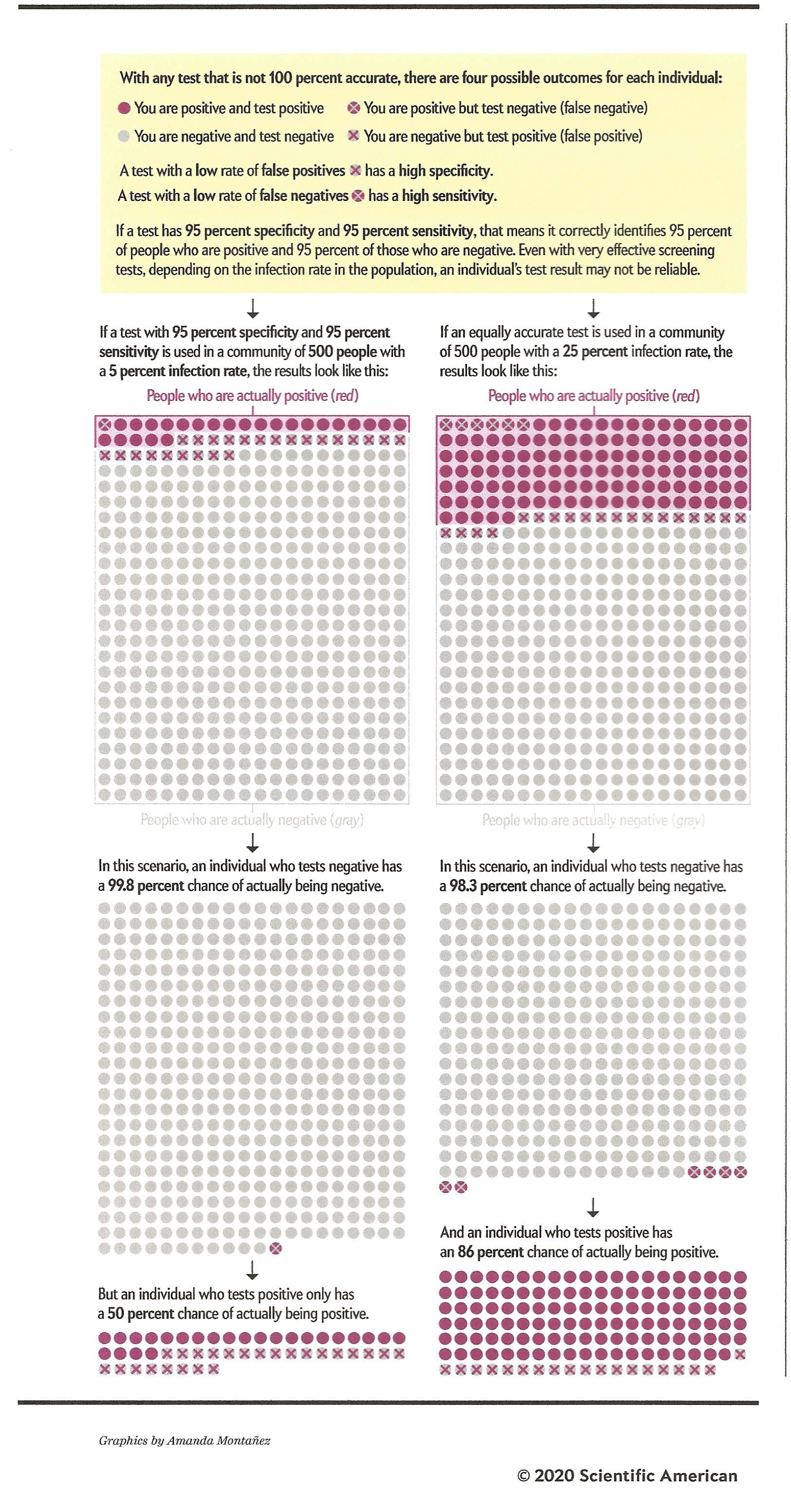
Z Value For 98 Confidence Interval Math

S is the standard deviation.

Z value for 98 confidence interval math. The z table and the preceding table are related but not the same to see the connection find the z value that you need for a 95 confidence interval by using the z table. Assuming the following with a confidence level of 95. However when you look up 1 96 on the z table you get a probability of 0. X z s n.

A confidence interval is a way of using a sample to estimate an unknown population value. The confidence interval is. Z is the chosen z value from the table above. For 95 the z value is 1 960.

Use that z value in this formula for the confidence interval. From 168 8cm to 181 2cm. Where z is the z value for the chosen confidence level x is the sample mean σ is the standard deviation and n is the sample size. X is the mean.

So far for 1 i have used the z table to look for 99 as i need 1 to the right of 2 33 and 1 to the left of 2 33 so 98 is between pm2 33. 1 96 first off if you look at the z table you see that the number you need for z for a 95 confidence interval is 1 96. C calculate the actual intervals. For estimating the mean there are two types of confidence intervals that can be used.

N is the number of observations. Giving me bar x pm 2 33 frac sigma sqrt n which provides me with a 39 08 to 49 36 confidence interval is this correct.